Model-based Geostatistics for Global Public Health

From Methodology Development to Policy Applications

Author
Affiliation

Emanuele Giorgi

University of Birmingham

My Background

  • PhD in Statistics and Epidemiology (Sep 2015)
  • MSc in Statistics (July 2012)
  • BSc in Statistics (April 2012)

Presentation Overview

  1. Neglected Tropical Diseases: an overview
  2. Model-based Geostatistics: Current and Future Research
  3. Informing Policy Decisions
  4. Capacity Building

Neglected tropical diseases

NTD endemic areas

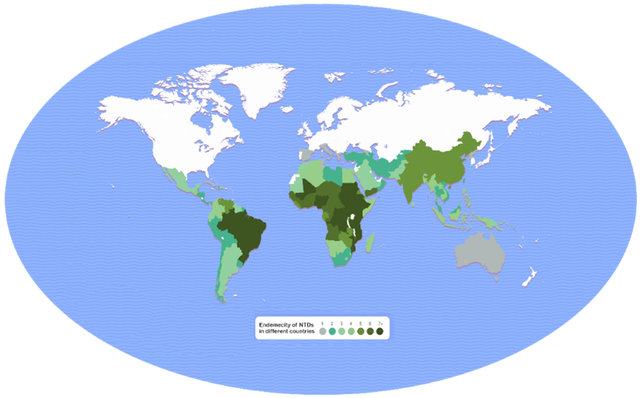
The impact of NTDs

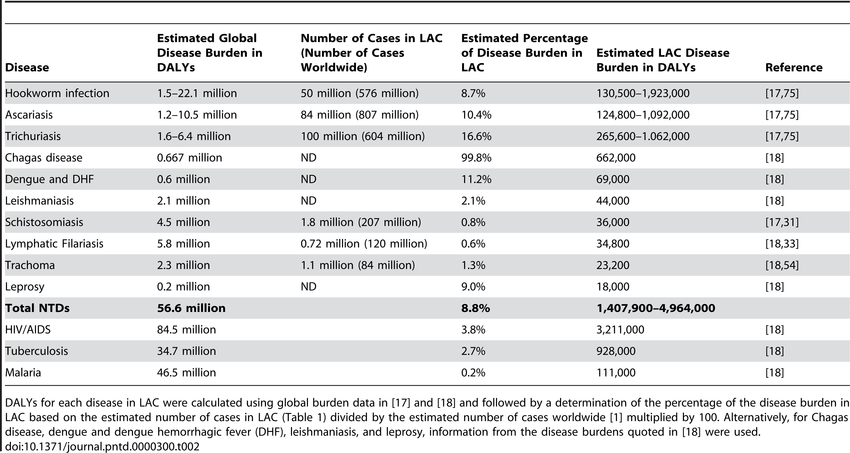
NTDs Risk Factors

Common risk factors:
- Poor sanitation and lack of clean water
- Limited healthcare access
- Poverty and overcrowding
- Exposure to disease vectors (e.g., mosquitoes, flies)
- Lack of education and awareness

From the mining industry to public health

(a) Danie Gerhardus Krige GCOB (26 August 1919 – 3 March 2013)

(b) Mining application of geostatistics

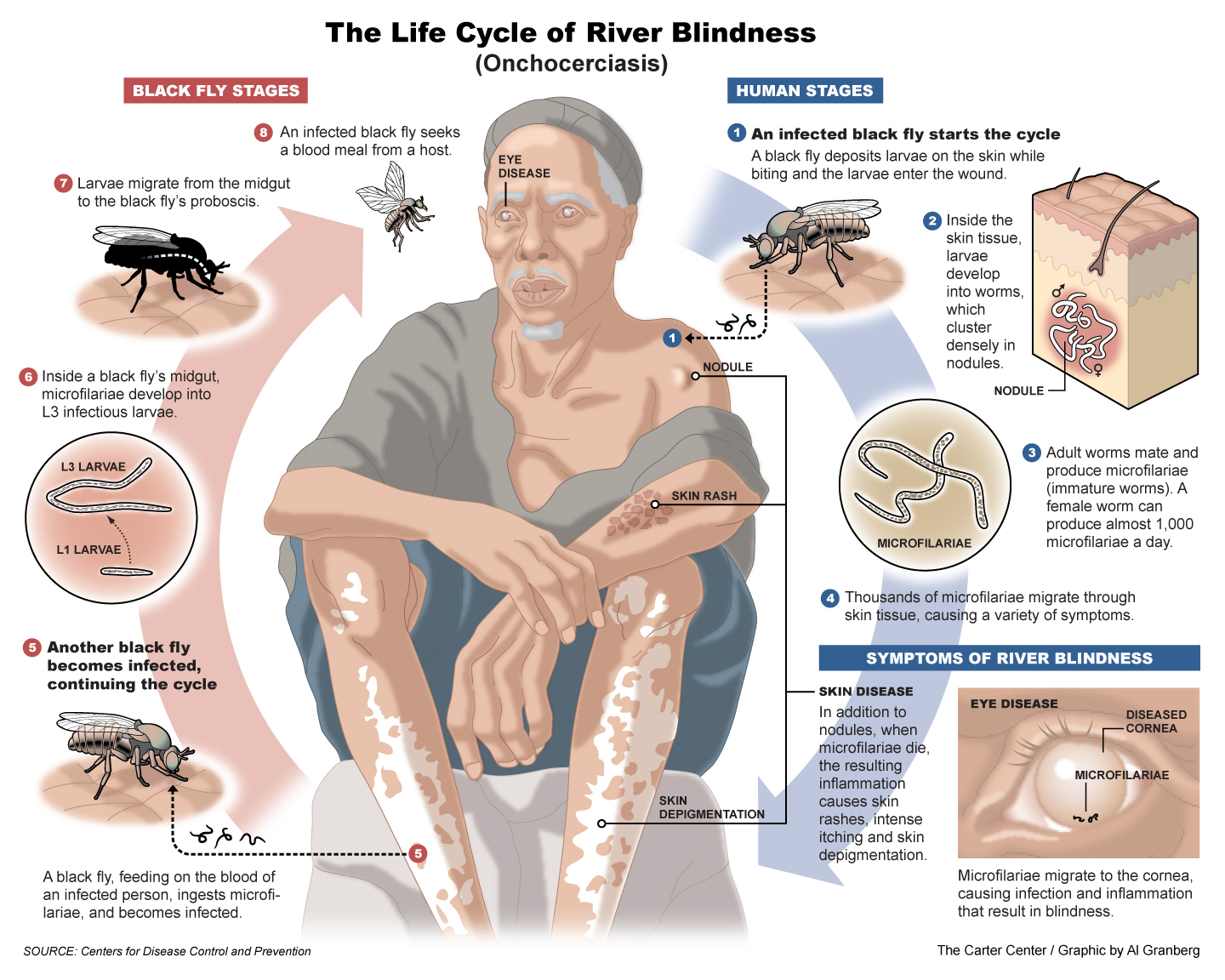
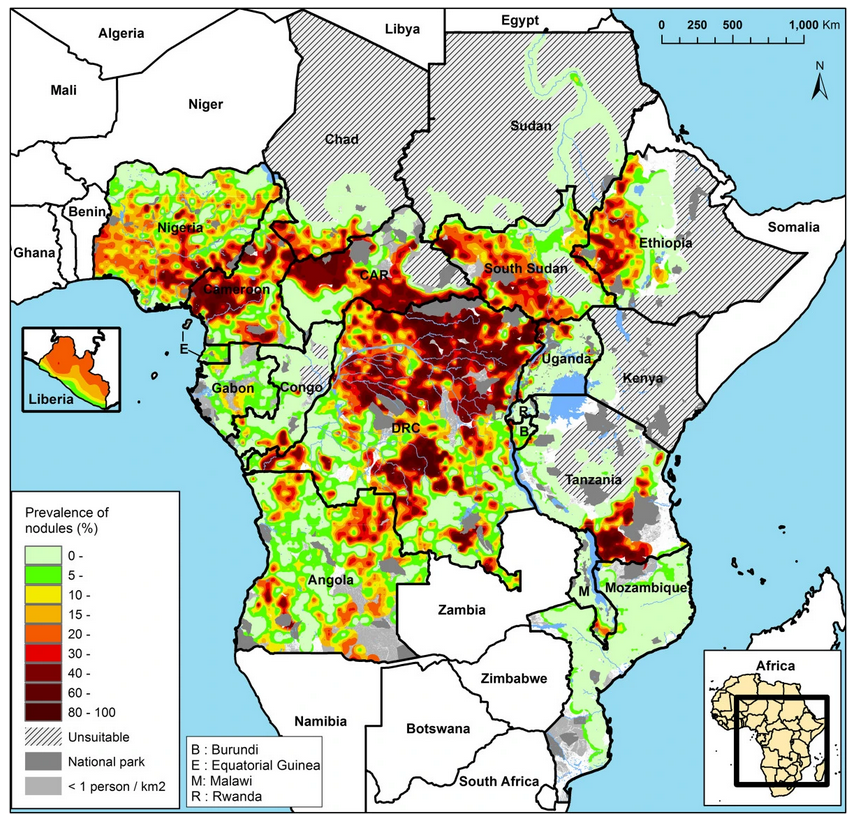
Riverblindness

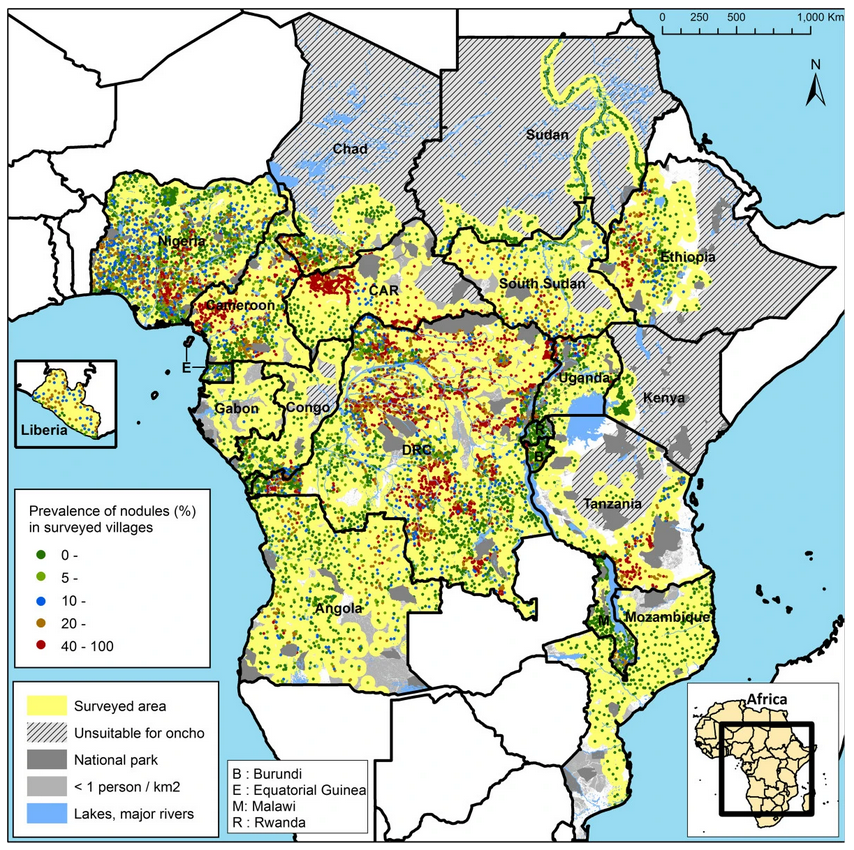
Mapping river-blindness

(a) Map of the observed prevalence of palpable nodules in the 14,473 surveyed villages.

(b) Map of the predicted prevalence.

The ingredients of a geostatistical model for prevalence mapping

  • Outcome: \(Y_i\) number of cases out \(n_i\) sampled

. . .

  • Locations: \(X = (x_1, \ldots, x_n)\)

. . .

  • Covariates (optional): \(d(x)\) (e.g. elevation, distance from waterways)

. . .

  • Spatial Gaussian process: \(S(x)\) (stationary and isotropic) \[ {\rm cov}\{S(x), S(x')\} = \sigma^2 \rho(||x - x'||; \phi) \] Example: \(\rho(u; \phi) = \exp\{-u/\phi\}\).

Putting all together

  • Conditional independence: \(Y_{i}\) conditionally on \(S(x_i)\) are mutually independent \(Bin(n_i , p(x_i))\)

. . .

  • The linear predictor \[ \log\left\{\frac{p(x_i)}{1-p(x_i)}\right\} = \beta_0 + d(x_i)^\top \beta + S(x_i) \]

. . .

  • The joint distribution: \([S, Y] = [S] [Y | S]\)

where \(Y=(Y_1, \ldots, Y_n)\) and \(S = (S(x_1), \ldots, S(x_n))\)

. . .

  • The likelihood function \[ L(\theta) = \int_{\mathbb{R}^n} [S] [Y | S] \: dS \] How do we approximate this intractable integral?

PrevMap and RiskMap

. . .

Giorgi, E. and Fronterre, C. (expected August 2025) Model-based geostatistics for global public health using R. Chapman and Hall/CRC. The R Series.

Identifying disease hotspots

  • Hotspot: riverblindness prevalence above \(20\%\)

. . .

  • Exceedance probability: \({\rm Prob}\{p(x) > 0.2 \: | \: Y \}\)

. . .

Extensions to spatio-temporal modelling

Question: Which spatio-temporal correlation structures are suitable for modelling disease prevalence data?

. . .

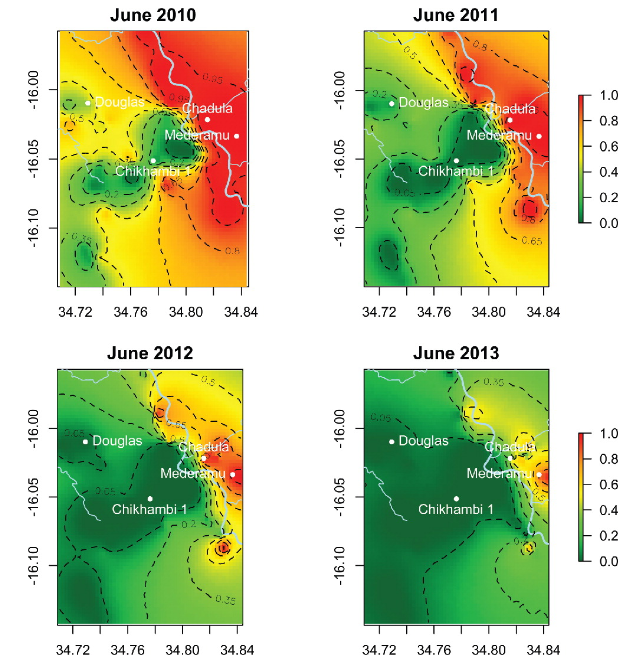
Giorgi, E., Diggle, P. J., Snow, R. W., Noor, A. M. (2018). Geostatistical methods for disease mapping and visualization using data from spatio-temporally referenced prevalence surveys. International Statistical Review. https://doi.org/10.1111/insr.12268

Combining data from multiple diagnostics

Questions: 1) How we predict a gold-standard diagnostic using cheap biased diagnostics? 2) How do we model the bivariate relationship between two complementary gold-standards?

. . .

Amoah, B., Diggle, P. J., Giorgi, E. (2019). A geostatistical framework for combining data from multiple diagnostic tests. Biometrics. doi:10.1111/biom.13142

Spatially structured zero-inflation

Question: How can we effectively model the bivariate relationship between disease suitability and disease prevalence?

. . .

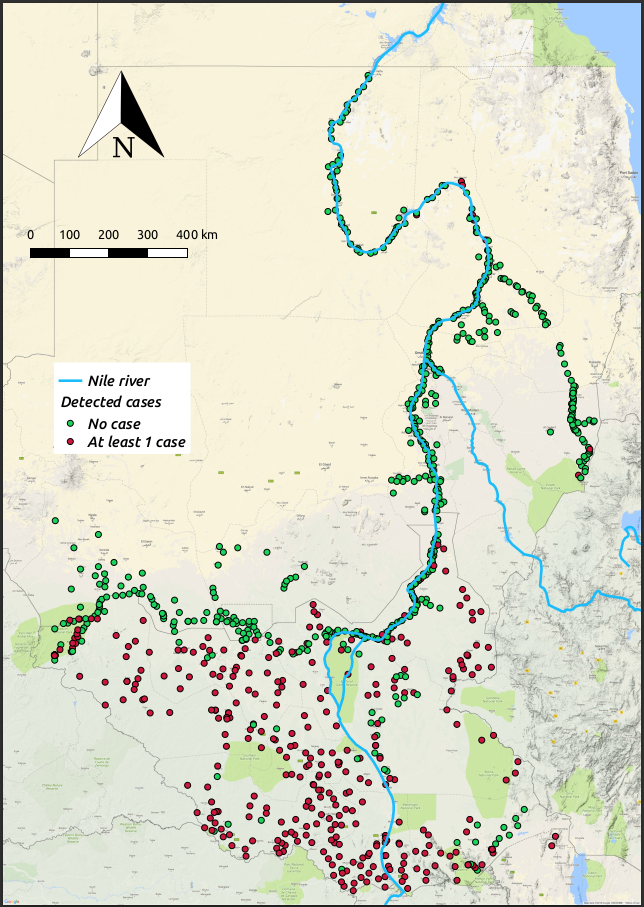
Diggle, P. J., Giorgi, E. (2016). Model-based geostatistics for prevalence mapping in low-resource settings (with discussion). Journal of the American Statistical Association. 111:1096-1120

Future methodological directions

  • Using multivariate geostatistical models to analyse serological data from multiple diseases

  • Incorporating mathematical models for the impact of interventions into geostatistical models

  • Developing more robust methods for the validation of geostatistical models for counts data.

  • Dealing with spatial and temporal misalignment in repeated cross-sectional survey data

Translation into policy: the case of trachoma

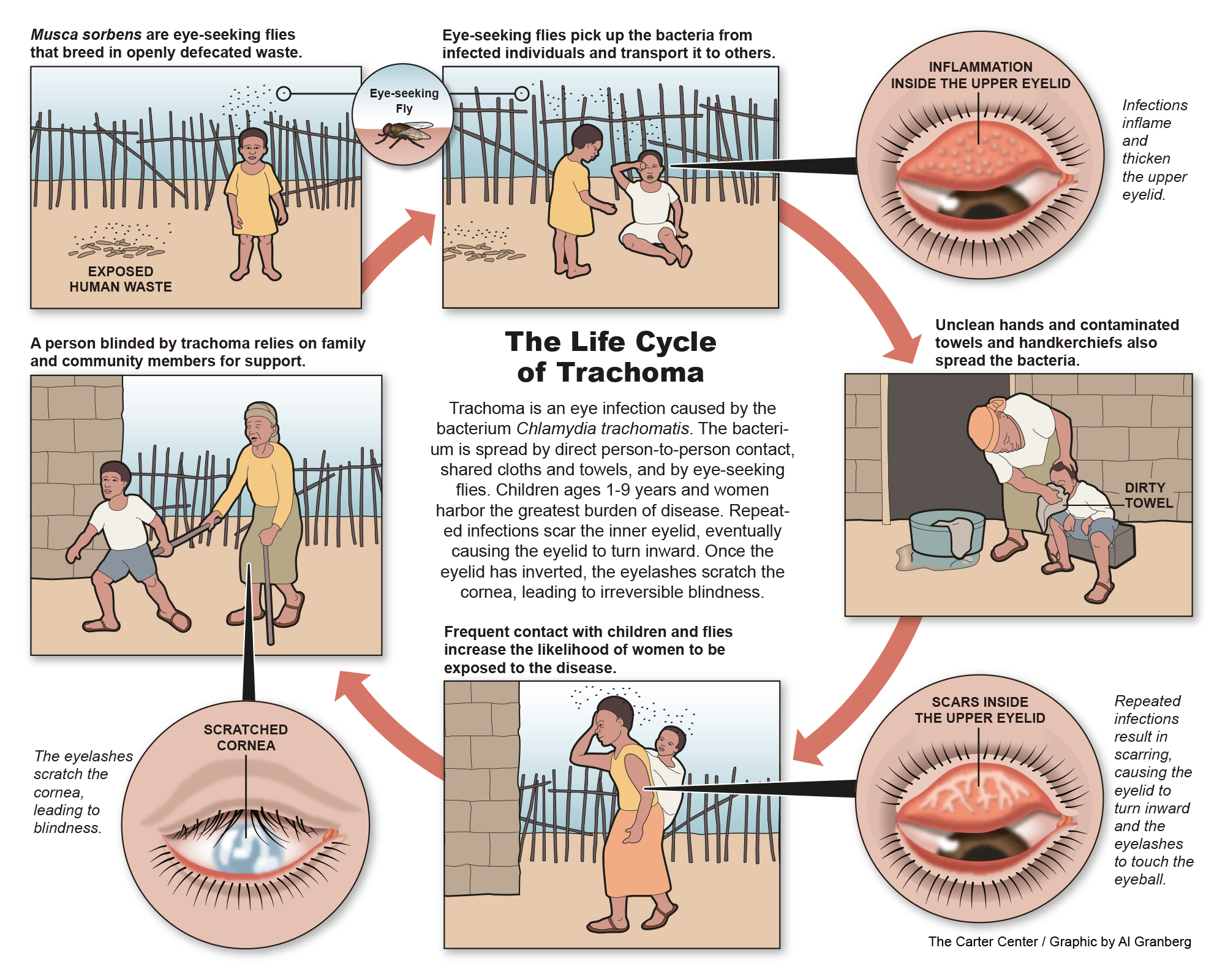
Informing the elimination of trachoma

Sasanami, M., et al. (2023). Using model-based geostatistics for assessing the elimination of trachoma. PLoS Neglected Tropical Diseases, 17(7): e0011476. https://doi.org/10.1371/journal.pntd.0011476

Challenges in Translating Geostatistics for Policy

  • Complexity of methods – Advanced models are difficult to interpret for non-specialists.

  • Data uncertainty – Policymakers may struggle to incorporate probabilistic estimates into decision-making.

  • Lack of user-friendly tools – Limited access to tools that allow interactive exploration of spatial predictions.

  • Lack of local geostatistical expertise – Few or no local experts support to support control programmes.

Engagement with policy makers

Technical meeting on geostatistical methods for trachoma elimination

Lancaster University, 4-5 March 2024

Engagement with policy makers

Technical meeting on capacity building

Lancaster University, 3-4 March 2025

A user-friendly app for malaria mapping

Link to Maplaria App

THANK YOU!

Let’s Connect
🔗 giorgistat.github.io
📧 e.giorgi@bham.ac.uk
📍Department of Health Sciences, University of Birmingham, Birmingham, UK